最小二乘法可谓是至关重要的数学工具

最小二乘法

基本思想

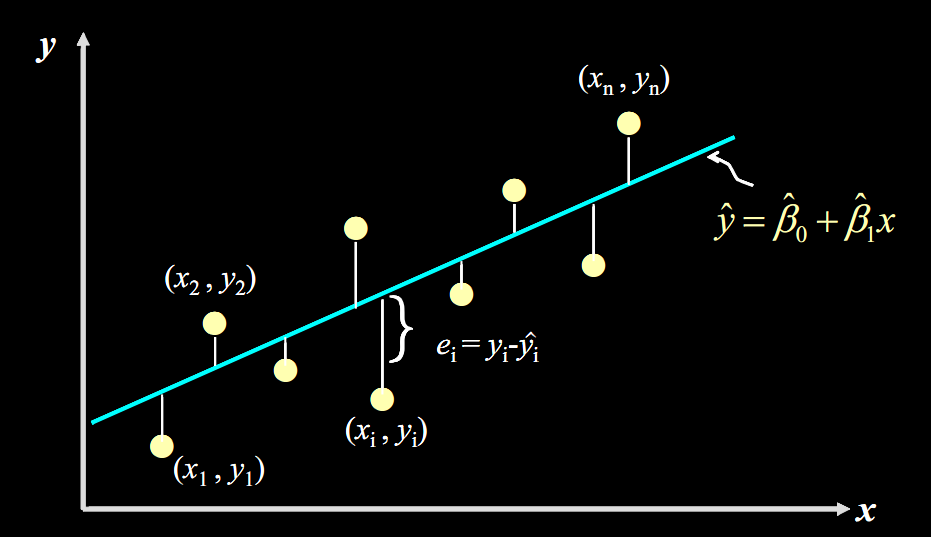
在最简单的一元线性函数拟合问题中，可以很直观得到目标函数：残差平方和

$$ \begin{aligned} \boldsymbol{\hat{\phi}}& =\quad\underset{\boldsymbol{\phi}}{\operatorname*{argmin}}\Big[\operatorname{L}[\phi]\Big] \\ &=\quad\underset{\boldsymbol{\phi}}{\operatorname*{argmin}}\left[\sum_{i=1}^{I}\left(\mathrm{f}[x_i,\boldsymbol{\phi}]-y_i\right)^2\right] \\ &=\quad\underset{\phi}{\operatorname*{argmin}}\left[\sum_{i=1}^I\left(\phi_0+\phi_1x_i-y_i\right)^2\right]. \end{aligned} $$ 要使得该目标函数最小，方法是朝着梯度下降的方向行进，这在机器学习中很常用

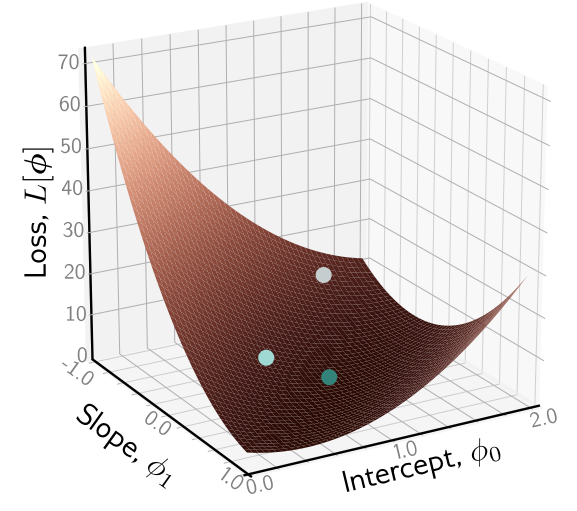
在数学上，最低点应该是一个极值点，对参数的偏导为0 $$ \begin{aligned}\frac{\partial L}{\partial\phi_0}&=2\sum_1^n\left(y_i-\hat{\phi_0}-\hat{\phi_1}x_i\right)=0\\\frac{\partial L}{\partial\phi_1}&=2\sum_1^n\left(y_i-\hat{\phi_0}-\hat{\phi_1}x_i\right)=0\end{aligned} $$

矩阵表示

如果用矩阵表示多元线性函数： $$ h_\phi(\mathbf{x})=\mathbf{X \phi} \ Y = \mathbf{X \phi} + V $$ 目标函数可定义为： $$ J(\phi)=\frac12(\mathbf{X}\phi-\mathbf{Y})^T(\mathbf{X}\phi-\mathbf{Y}) $$ 这里的二分之一是为了去掉下面求导的2

同样求偏导： $$ \frac\partial{\partial\phi}J(\phi)=\mathbf{X}^T(\mathbf{X}\phi-\mathbf{Y})=0 \ \mathbf{X}^T\mathbf{X}\phi=\mathbf{X}^T\mathbf{Y} $$ 解这个矩阵方程，得到的$\mathbf{\hat{\phi}}$ $$ \mathbf{\hat{\phi}}=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y} $$

加权

加权最小二乘，一般在不等精度测量中使用

加权加在最后残差不是简单平方和，而是加权平法和

这样的矩阵表示是： $$ J(\phi)=\frac12 (\mathbf{X}\phi-\mathbf{Y})^T \mathbf{P} (\mathbf{X}\phi-\mathbf{Y}) $$ 解为： $$ \mathbf{\hat{\phi}}=(\mathbf{X}^T\mathbf{P}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{P}\mathbf{Y} $$ 一般来说，这个权值不是随便定的，而是根据协方差矩阵来的

随机误差协方差矩阵：

$$ \mathrm{R}=\mathrm{E}(\mathrm{v}^\mathrm{T})= \begin{pmatrix} \sigma_1^2 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_\mathrm{k}^2 \end{pmatrix} $$

则权值即为协方差倒数：$P = R^{-1}$ $$ \mathrm{J}=\frac{\varepsilon_1^2}{\sigma_1^2}+\frac{\varepsilon_2^2}{\sigma_2^2}+…+\frac{\varepsilon_k^2}{\sigma_k^2}=\varepsilon^T\mathrm{R}^{-1}\varepsilon $$

非线性情况

对于非线性方程，也是想将其变为线性方程来求

线性回归

回归的含义是指预测连续量，区别于分类问题

线性回归也就是指用线性函数预测，通过已有数据结合最小二乘法拟合出直线，这就是线性回归，在机器学习中这个过程就是训练

概统角度

若测量误差服从高斯分布，只有随机噪声，那么认为测量量是无偏的： $$ E(Y) = X \phi $$ 则有： $$ E(\hat{\phi}) = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{X} \phi = \phi $$ 所以也是无偏的，即极大似然估计