LAMBDA算法
LAMBDA算法的大概原理和RTKLIB中的代码
LAMBDA算法
理论基础
整体的过程是:z变换到新空间以去相关 $\rightarrow$ 在新空间搜索最佳整数模糊度组合(更高效)$\rightarrow$ 变换回原空间
载波相位测量
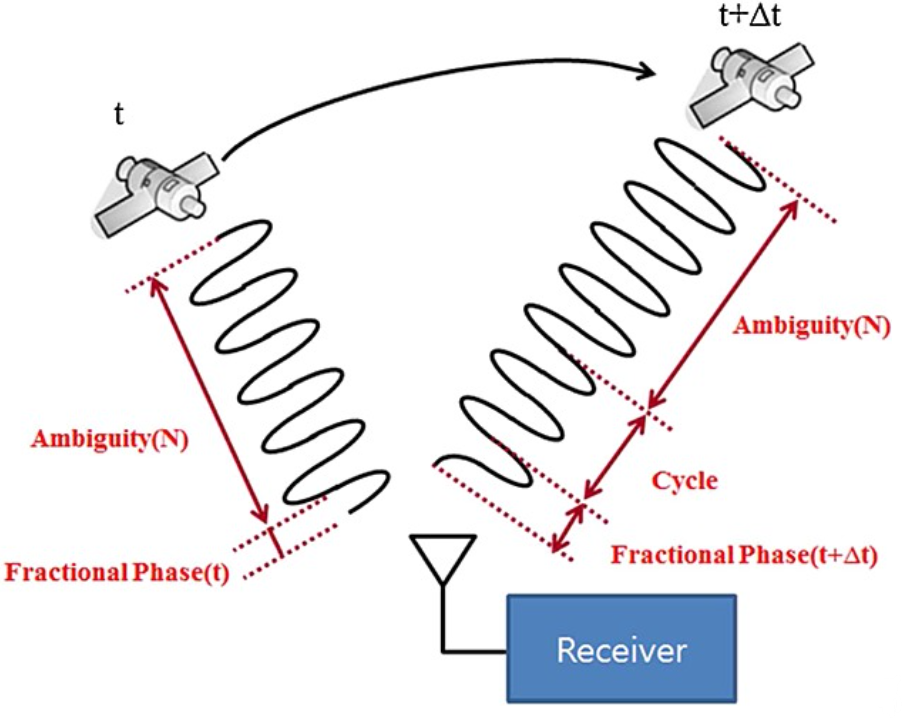
理想情况下,卫星在 $t$ 时刻发送其当前的相位信息,至 $t+\delta t$ 时刻接收机测到,接收机有一个和卫星同步的波,测量即可得到此时卫星上的相位,那么,两者之差 (fraction)乘以波长,加上未知的整数部分 (Ambiguity)即可得到距离
但是由于卫星是运动的,运动过程中距离又在变化,所以还有一个 cycle 部分,接收机对卫星进行信号跟踪一段时间,通过积分可以求出这个cycle
$$
Cycle(t+\delta t) = Int[\int_{t}^{t + \delta t} \delta f ~\mathrm{dt} + F(t)]
$$
但是如果有短时间遮挡等原因导致时区最终,这里算出来的值就会有误差,就是周跳,周跳有周跳的检测方法(挖坑)
测量相位只能得到周内的小数部分 (fraction),所以整数部分是未知的,也是无法测量的
瞬时的测量能够得到小数部分,如果保持追踪,载波相位应该是连续变化的
注:我们把位置信息叫做解,把载波相位未知的整数部分叫做整周模糊度,把EKF中所有带估计量整体向量叫做状态量
通过EKF(或者最小二乘法)已经有了浮点模糊度 $\hat{a}$,它们很遗憾不是整数,所以针对多个测量中的模糊度,要找一套整数组合 $\check{a}$ ,这就是模糊度固定(一般把整数叫做fix)
变换到新空间以降相关
最优的整数组合 $\breve{a}$ 应当满足目标函数最小的原则,目标函数还是残差平方和,设协方差矩阵为 $Q_{{\hat{a}}}$ $$ \breve a = argmin | (\hat{a} - \breve{a})^{T} Q_{\hat{a}}^{-1} (\hat{a} - \breve{a}) $$ 这个公式可参考最小二乘法,其实就是残差平方和的矩阵形式
相关性就是协方差矩阵体现,应尽可能使得近似对角矩阵,这样相关性才低。通过Z变换来实现: $$ \hat{z} = Z \hat{a} \ Q_{\hat{z}} = Z Q_{\hat a} Z^T \ $$ 那如何找这个 $Z$:
要进行Choleskey分解:$Q_{\hat{a}} = L D_{\hat{a}} L^T \quad Q_{\hat{z}} = \bar L D_{\hat{z}} \bar L^T$,其中 $L$ 是下三角矩阵且对角线上元素均为1,$D$ 是对角矩阵
LAMBDA算法要求:(为什么要这样也不清楚)
- $\bar L$ 尽可能对角化(非对角元素小于0.5)
- $Q_{\bar{a}}$ 尽可能按序排列
所以后面会有降低和排序的操作
参考:

模糊度搜索
在新空间里面采取搜索算法(DFS等)找到最合适的解
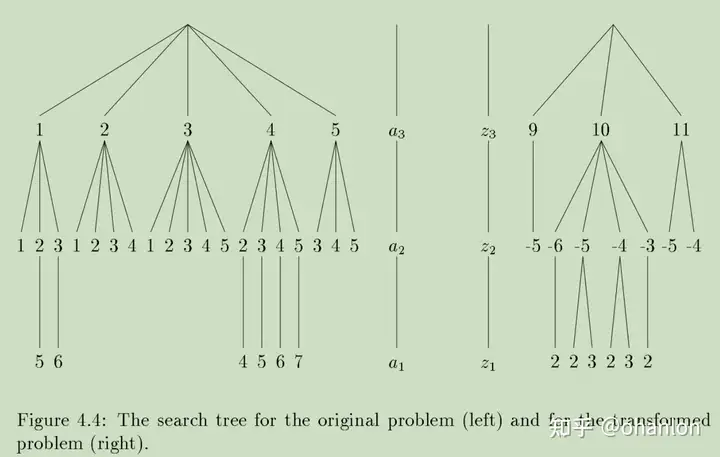
较之原空间,搜索效率大大提高
检验
就是比的残差平方和,次优解与最优解之比越大说明最优解这个最低值越突出,也说明越可靠