神经网络入门-MINIST（未完待续）

2023-07-17 in AI

Contents

base on 《Make Your Own Neural Network》by Tariq Rashid, 中文版

神经网络

理论

结构

神经元不会理解做出反应，而是会抑制输出，直到输入大到超过阈值才触发输出（避免噪声）

所以有激活函数，直观来讲输入输出是一个阶跃函数，但一般改进为S函数：平滑更符合自然规律

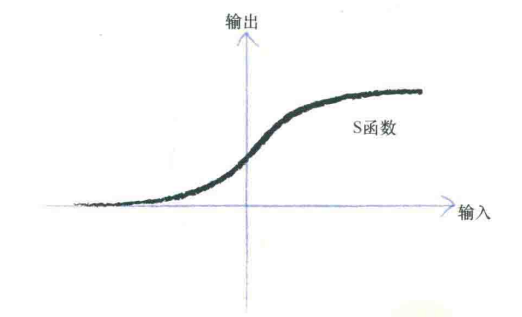
多个输入信号被组合成更强大的输入信号

神经元输出传递也是后面神经元的输入：

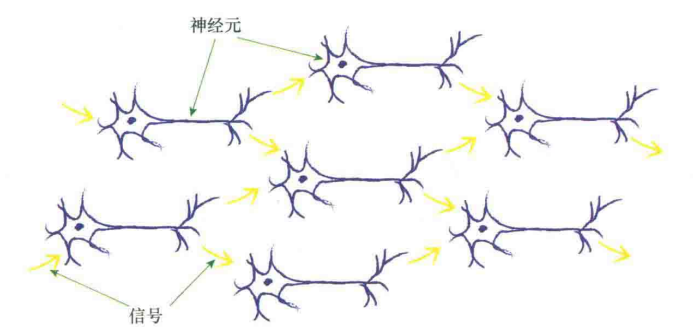
于是我们对它进行分层设计：

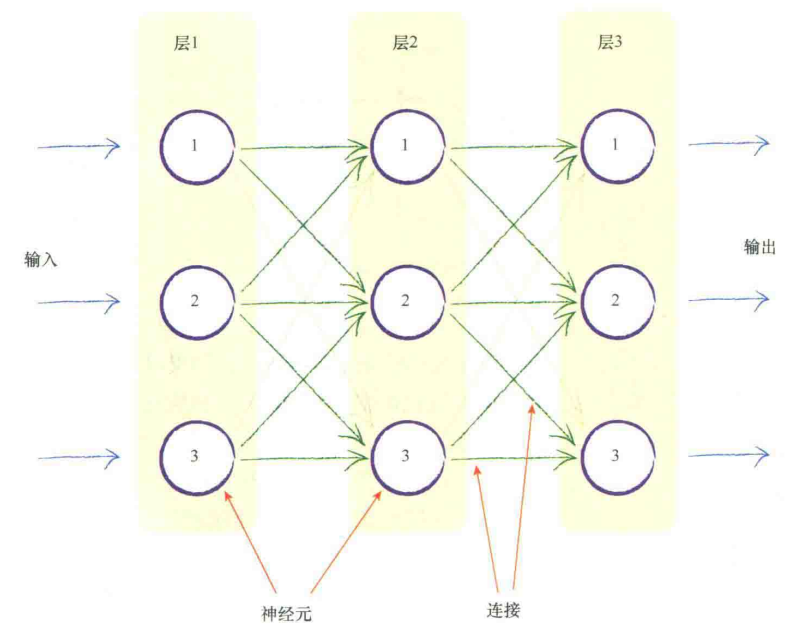
现在需要进行学习调整其中的参数，其中最简单的方法就是各个边的权重

一开始权重取随机值

输出

第一层仅接受输入

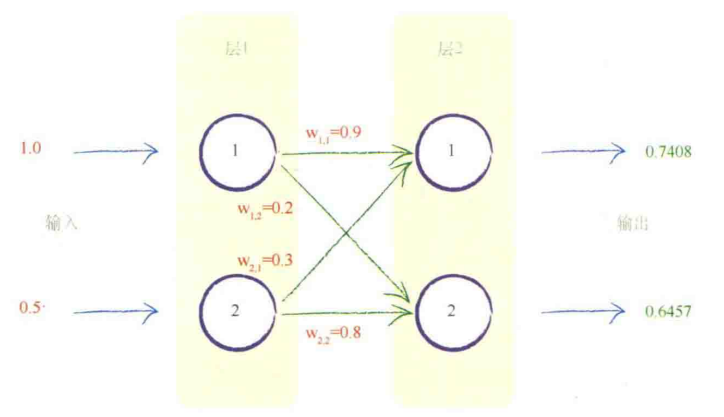
这个计算输出可以用矩阵来简化

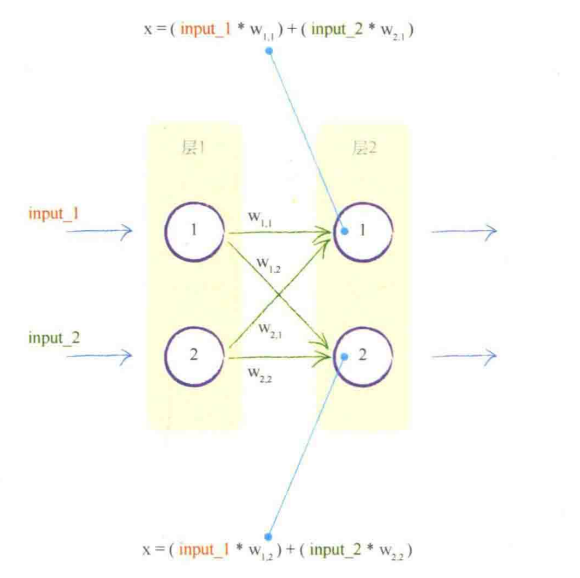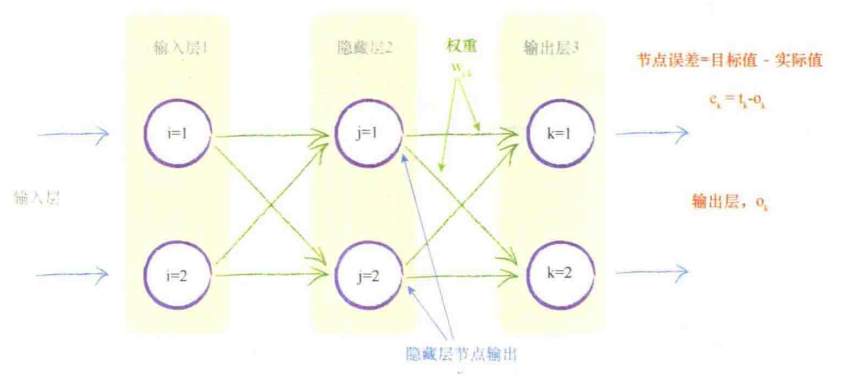
$$ X = WI \\ O = sigmoid(I) $$ 对于三层网络，一般称中间那层为隐藏层

输入层-隐藏层，隐藏层-输出层之间都有这个关系

反向传播

将样本的结果和计算结果比较得到误差

将误差分给多个输入优化它们的权重

这就是反向传播：

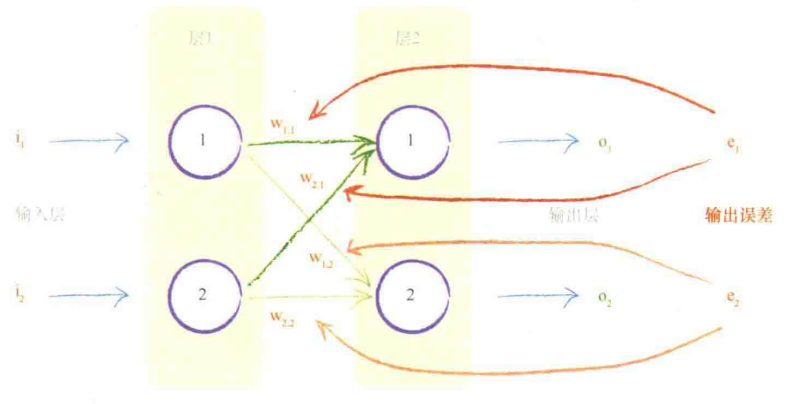
相当于翻过来输出当输入，得到每个节点的误差值（尽管中间节点并没有一个目标值）

权重更新：梯度下降法

找到总误差的最小值点，这里定义总误差为： $$ E = e_1^2 + e_2^2 +…+e_n^2 $$ 这样避免了相互抵消

以梯度下降的方向更新权重，需要求出梯度、选择合适的步长，步长的选择影响还是很大的：

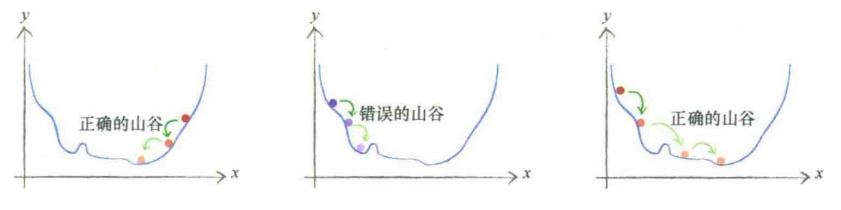
步长以学习率$\alpha$来反应： $$ w_{j,k} = w_{j,k} - \alpha\frac{\partial E}{\partial w_{j,k}} $$ 现在只考虑隐藏层和输出层之间的权重：

$$ E = \sum (t_k -o_k)^2 \\ \frac{\partial E}{\partial w_{j,k}} = \frac{\partial E}{\partial o_k} \cdot \frac{\partial o_k}{\partial w_{j,k}} $$ $t_k$是目标值是常数，进一步化简，得到表达式：

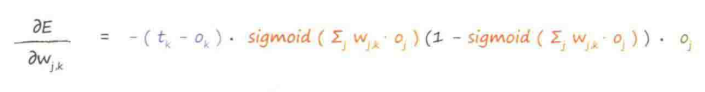
这是隐藏层与输出层之间的权重，而输入层与隐藏层之间的权重，通过节点的“误差”代换掉即可，这里用到了对称性的思想

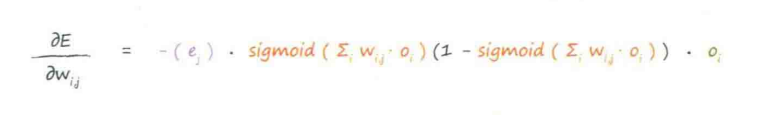
总之，我们统一为：

实践

训练集：用于训练

测试集：评价好坏

输出中最大的那个的编号作为结果

最理想的输出是 [0, 0, …1, 0, 0]这样的，但实际不可能(sigmoid)上下界

改进

多次重复训练叫做世代

epoch和学习率会影响性能：

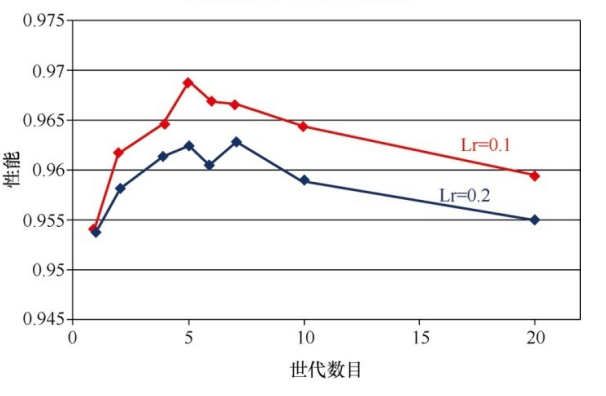
网络的结构（隐藏层数量、层数）

其它

自己的手写数字

反向查询：从label反推Image

对图像旋转后对结果的影响

源码：

# build a class
import numpy
import scipy.special
class neuralNetwork:
    # initial parameters and something else
    def __init__(self, inputnodes, hiddennodes, outputnodes, learningRate) -> None:
       # the 3 layers
       self.inodes = inputnodes
       self.hnodes = hiddennodes
       self.onodes = outputnodes
       # learning rate alpha
       self.lr = learningRate
       # weight 正态分布
    #    self.wih = numpy.random.rand(self.hnodes, self.inodes) - 0.5
    #    self.who = numpy.random.rand(self.onodes, self.hnodes) - 0.5
       self.wih = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))
       self.who = numpy.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))
       # activate function
       self.activate_function = lambda x: scipy.special.expit(x)
    
    # train: update weights
    def train(self, inputs_list, targets_list):
        # convert to Array (why 2D?)
        inputs = numpy.array(inputs_list, ndmin=2).T
        targets = numpy.array(targets_list, ndmin=2).T
        # matrix computing
        hidden_inputs = numpy.dot(self.wih, inputs)
        hidden_outputs = self.activate_function(hidden_inputs)

        final_inputs = numpy.dot(self.who,hidden_outputs)
        final_outputs = self.activate_function(final_inputs)

        output_errors = targets - final_outputs
        # go back
        hidden_errors = numpy.dot(self.who.T, output_errors)
        input_errors = numpy.dot(self.wih.T, hidden_errors)

        # update
        self.who += self.lr * numpy.dot(output_errors * final_outputs 
                                        * (1.0 - final_outputs), numpy.transpose(hidden_outputs))
        self.wih += self.lr * numpy.dot(hidden_errors * hidden_outputs 
                                        * (1.0 - hidden_outputs), numpy.transpose(inputs))
    # query: take input and compute output
    def query(self,inputs_list):
        # convert to Array (why 2D?)
        inputs = numpy.array(inputs_list, ndmin=2).T
        # matrix computing
        hidden_inputs = numpy.dot(self.wih, inputs)
        hidden_outputs = self.activate_function(hidden_inputs)

        final_inputs = numpy.dot(self.who,hidden_outputs)
        final_outputs = self.activate_function(final_inputs)

        return final_outputs




# set parameters
input_nodes = 784 # 28*28
hidden_nodes = 100
output_nodes = 10

learning_rate = 0.3

nn = neuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)
training_data_file = open("mnist_dataset/mnist_train_100.csv", "r")
training_data_list =training_data_file.readlines()
training_data_file.close()

epochs = 5
for e in range(epochs):
    for record in training_data_list:
        all_values = record.split(",")
        inputs = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01
        # ideal and practial targets
        targets = numpy.zeros(output_nodes) + 0.01
        targets[int(all_values[0])] = 0.99

        # start training!
        nn.train(inputs, targets)
    print("epoch", e, "done")
    
test_data_file = open("mnist_dataset/mnist_test_10.csv", "r")
test_data_list =test_data_file.readlines()
test_data_file.close()
# test the neural network
# scorecard for how well the network performs, initially empty
scorecard = []
# go through all the records in the test data set
for record in test_data_list:
    # split the record by the ',' commas
    all_values = record.split(',')
    # correct answer is first value
    correct_label = int(all_values[0])
    print(correct_label, "correct label")
    # scale and shift the inputs
    inputs = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01
    # query the network
    outputs = nn.query(inputs)
    # the index of the highest value corresponds to the label
    label = numpy.argmax(outputs)
    print(label, "network's answer")
    # append correct or incorrect to list
    if (label == correct_label):
        # network's answer matches correct answer, add 1 to
        scorecard
        scorecard.append(1)
    else:
        # network's answer doesn't match correct answer, add 0 to
        scorecard
        scorecard.append(0)
        pass
print(scorecard)
scorecard_array = numpy.asarray(scorecard)
print ("performance = ", scorecard_array.sum() / scorecard_array.size)

依赖文件：

mnist_test_10.csv

mnist_train_100.csv

作者repo